从直觉上来看,大家都知道延时与利用率是一个正比关系,但这个关系是线性的,还是指数的?可能就没多少人能说的清楚了。这篇文章,我们只从理论分析入手,试图一步步推导出他俩的关系公式。
1. 预备知识
专门研究这个领域的理论叫排队论,它是一种数学和概率论的分支。这次的理论推导,我们并不需要成为数学博士才能掌握,只需要了解其中的两个基本定理,就能得出一个简易可用的模型(感谢GPT4不厌其烦的答疑,感谢我们生活的时代,技术让知识触手可及)。
1.1. Little’s Law
Little’s Law 是排队论中的一个基本定理,这里的 Little 完全是字面意思,取自于作者 John D.C. Little ,跟逻辑意义上的大小无关。它用于描述一个处于稳定状态下的排队系统中请求数、到达率以及平均逗留时间之间的关系:
$$L = λW$$
其中:
- L:系统中的平均请求数(同时包括正在接受服务的请求和等待服务的请求)。
- λ:单位时间内到达系统的请求数量,即到达率。
- W:请求在系统中的平均逗留时间(包括逗留时间和服务时间),即我们感知到的延迟。
而稳定状态是指,从长期来看,到达率和服务率之间达到了动态平衡,否则就会出现队列无限增长或者长期排空的现象。从这个前提条件也可以看出,Little's Law是一个基于统计平均值的定理,它可能无法反映某些特定个体、或者特定时间点的情况。
1.2. M/M/1 模型
M/M/1 模型是最基本的排队模型,其中的第一个M(Markovian)表示到达率服从泊松分布(Poisson Distribution),第二个M表示服务速率也服从泊松分布,而数字1表示系统只有一个服务器。在这个模型中,平均逗留时间W可以通过以下公式计算:
$$W = \frac{λ} {μ * (μ - λ)}$$
这里新出现的参数µ表示请求完成的速度。
1.2.1 推导过程
M/M/1 模型的公式可以用归纳法推导出来:
设 X(t) 表示在时间 t 时,系统中的请求数量(包括正在接受服务的请求和正在等待服务的请求)。这是一个连续时间马尔可夫链(CTMC),其中每个状态变换(请求到达或请求离开)都是一个泊松过程。
考虑平稳状态下的情形,系统的到达请求数等于离开请求数。对于状态 i(即系统中的请求数量为 i)和 j(= i±1),平稳状态下的平衡方程如下:
|
|
其中P(X=i)和P(X=j)分别代表状态 i 和 j 的概率。这个方程的含义是,系统中达到某个状态的速率(即到达速率 λ 乘以该状态的概率 P(i))应该等于离开该状态的速率(即离开速率 μ 乘以下一个状态的概率 P(j))。
从不含请求的状态(空闲状态)开始,设空闲状态的概率为 P0,可以递归出如下关系:
|
|
以概率 P0 为基准,将上述公式翻转一下,就可以得出每个状态 i 的概率(记为 Pi):
|
|
由于所有状态的概率之和应该等于 1,即ΣP(X=i) = 1,我们可以得到:
|
|
上式是一个等比数列求和公式。已知 λ < μ(否则系统将不稳定),所以求和结果为:
|
|
上式中1 / (1 - λ/μ)是等比数列求和的结果,通过求解与 P0 相关的这个等式,我们可以得到:
|
|
现在我们已经找到了空闲状态(状态 0)的概率 P0,算是完成了第一个 Milestone。由于我们感兴趣的是系统中的平均请求数L,而它可以按如下方式计算出来:
|
|
对于i = 1, 2, 3, ...求和,得出:
|
|
上式中括号内是另一个等比数列,求和结果为:
|
|
代入 P0 和以上等比数列求和结果,计算 L:
|
|
已知P0 = (μ - λ) / μ,代入 L 的表达式:
|
|
我们可以继续简化 L 的表达式,得到:
|
|
再结合上面的Little's Law(L = λ * W),我们就可以消掉参数L:
|
|
从而得到W与到达和离开速率之间的关系,这就是上面的M/M/1 模型的计算公式。
1.3. 系统利用率
利用率ρ是一个描述服务器负载情况的指标,比如我们常用 CPU 利用率、网卡利用率来描述服务器某一维度的负载情况。从更广义的角度来说,利用率可以表示为服务器处于繁忙状态的时间与总时间的比例,因此我们得到了平均意义上的利用率的计算公式:
$$ρ = \frac{λ} {μ}$$
2. 串联起来
铺垫了这么久,终于可以切入正题了 —— 我们感兴趣的是延时与利用率的关系,在M/M/1 模型中,我们计算出的平均逗留时间W可以看做平均延时,再将上面的ρ的表达式代入其中就得到这两者的关系:
$$W = \frac{ρ} {μ * (1 - ρ)}$$
从这个公式中,我们可以分析到,在给定的处理能力(μ)下,延时W确实与利用率ρ成正比,但这不是一个简单的线性关系,而是分式关系。当利用率ρ接近 1 时,系统处于饱和状态,延时W会急速增加。这是因为服务器正在达到其处理能力的极限,任何新到达的请求都可能导致更长的等待时间。
2.1. 感性认识
有图有真相,在系统处理能力μ=100的情况下,我们画出了ρ和W的关系图:
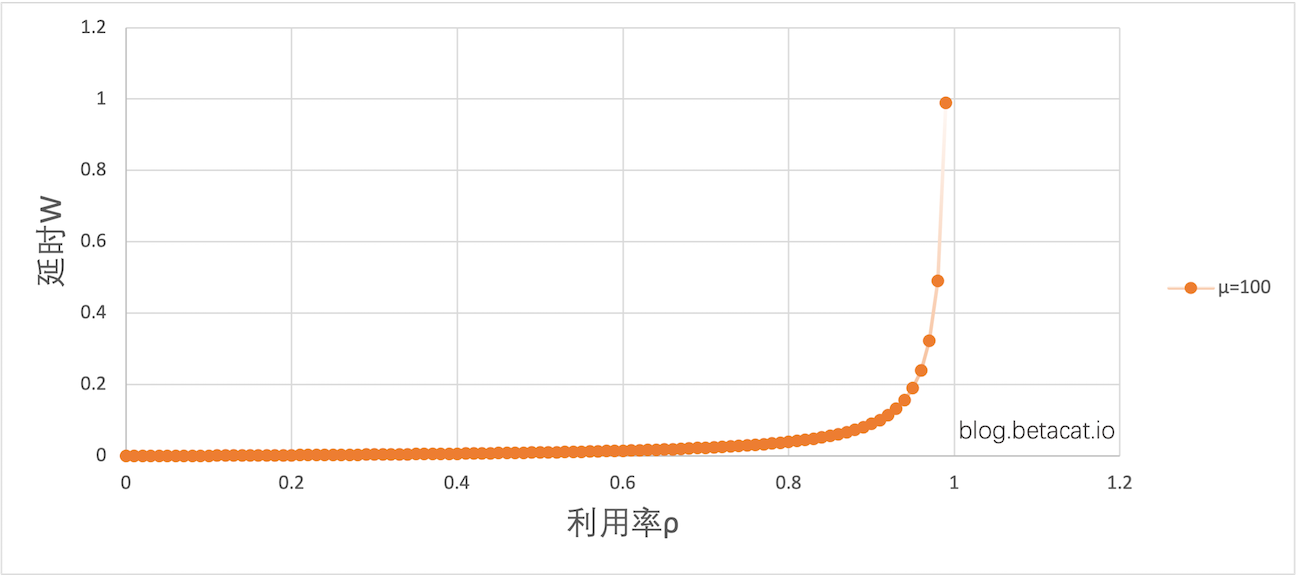
并且采样了几个典型的点位:
| 利用率 | 延时 | 增长 |
|---|---|---|
| 0.2 | 0.0025 | - |
| 0.3 | 0.0042 | 68% |
| 0.4 | 0.006 | 42% |
| 0.5 | 0.010 | 66% |
| 0.6 | 0.015 | 50% |
| 0.7 | 0.023 | 53% |
| 0.8 | 0.040 | 73% |
| 0.9 | 0.090 | 125% |
| 0.99 | 0.99 | 1000% |
可以看到,在0.8之前,利用率每提升 10 个百分点,延时就会增加 60% 左右,但利用率一旦超过0.8,延时急剧上升,且增速越来越快。在 0.9~0.99 这个区间内,延时甚至增加了 11 倍。
这就是为什么,我们会有个不成文的惯例 —— 系统的各项指标使用率都不要超过 80%。
3. 总结
这里虽然我们用了简化版的模型,但实际数据绘制出来的图形跟这个模型是非常接近,大家有兴趣可以自己压测对比一下,油管上有个视频也得出了相同的结论。
另外,从上面推导出来的理论公式,我们也可以扩展出几个与直觉相符的结论:
- 系统处理能力(
μ)与延迟(W)成反比,提升处理能力后,也能线性的减少访问延迟。 - 吞吐与延迟成正比,所以有人认为,同一个集群不可能同时满足低延迟和高吞吐的需求,只能做取舍,具体解释如下:
- 低延迟意味着低利用率,即希望系统没有排队现象,请求来了立即就得到处理,无需等待。
- 高吞吐意味着高使用率,即希望系统队列中始终有可用请求,这样各种资源才不会有空闲的时间,系统始终处于忙碌状态。